排序算法分为两大类,一是内部排序,即数据记录在内存中进行排序,另一个是外部排序,主要是因排序的数据很大,一次不能容纳全部的排序记录,在排序过程中需要访问外存。
内部排序
内部排序算法主要分为如下5类:
- 归并排序;
- 交换排序(包括快速排序和冒泡排序);
- 选择排序(包括堆排序和简单选择排序);
- 基数排序;
- 插入排序(包括希尔排序和直接插入排序)。
归并排序
归并排序(merge sort)是创建在归并操作上的一种有效的排序算法。1945年由John von Neumann(约翰·冯·诺伊曼)首次提出。
该算法是采用分治法(Divide and Conquer)的一个非常典型的应用,且各层分治递归可以同时进行。它是一个稳定的排序算法。绝大多数语言内置排序的首选算法。
归并排序的核心思想是围绕“归并”两字,先通过递归地分解数列,然后在合并数列就完成了归并排序。具体如下:
- 先将数组分成A、B两组,将A,B组各自再分成二组。依次类推。
- 其次就是如何将两个有序数列合并。这个非常简单,只要比较两个数列的第一个数,谁小就先取谁,取了后就在对应数列中删除这个数。然后再进行比较,如果有数列为空,那直接将另一个数列的数据依次取出即可。
时间复杂度
归并排序的效率是比较高的,设数列长为N,将数列分开成小数列一共要log2N步;合并有序数列的过程,时间复杂度可以记为O(N),故总共为O(N*log2N)。
空间复杂度
由于归并排序在归并过程中需要与原始序列同样数量的存储空间存放归并结果以及递归时深度为log2N的栈空间,因此空间复杂度为O(N+log2N)。
归并排序过程
以数组[50,10,90,30,70,40,80,60,20]为例:
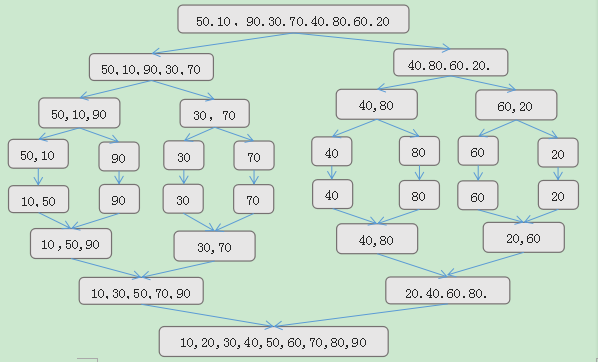
也就是说,归并排序是一种比较占内存,但却效率高且稳定的算法。
在Java、Python等诸多语言的标准库提供的排序实现都是归并排序,且是升级版的归并排序,叫TimSort,是Tim Peters在2002年设计的该算法。
快速排序
快速排序(quick sort)又称划分交换排序(partition-exchange sort),简称快排,是一种高效的排序算法。最早由英国计算机科学家、图灵奖得主Charles Antony Richard Hoare(查尔斯·安东尼·理查德·霍尔 爵士)在1962年提出的。
在平均状况下,排序n个项目要O(nlogN)次比较。在最坏状况下则需要O(N^2)次比较,但这种状况并不常见。事实上,快速排序通常明显比其他算法更快,因为它的内部循环(inner loop)可以在大部分的架构上很有效率地达成。
快速排序使用分治法(Divide and conquer)策略来把一个序列(list)分为两个子序列(sub-lists)。
算法的步骤如下:
- 从数列中挑出一个元素,称为“基准”(pivot);
- 重新排序数列,所有比基准值小的元素摆放在基准前面,所有比基准值大的元素摆在基准后面(相同的数可以到任何一边)。在这个分区结束之后,该基准就处于数列的中间位置。这个称为分区(partition)操作;
- 递归地(recursively)把小于基准值元素的子数列和大于基准值元素的子数列排序。递归到最底部时,数列的大小是0或1,也就是已经排序好了。
Java实现
import java.util.Arrays;
public class QuickSort {
private static int compareTimes = 0;
// 递归,先分治、后递归
public static void quickSort(int[] data, int low, int high) {
if (low < high) {
int index = partition(data, low, high);// 获取分割点
quickSort(data, low, index - 1);// 分治后的下游排序
quickSort(data, index + 1, high);// 分治后的上游排序
}
}
// 分治,将key放在应排的位置,并获取该位置
private static int partition(int[] data, int low, int high) {
int pivot = data[low];// 以第一个元素作为基准值
while (low < high) {
while (low < high && data[high] > pivot) {// <1> 从高位向下找到比关键值不大于的位置值
high--;
compareTimes++;
}
data[low] = data[high];// <2> 高位不大于关键值的数赋予关键值的位置
while (low < high && data[low] < pivot) {// <3> 从低位向上找到比关键值不小于的位置值
low++;
compareTimes++;
}
data[high] = data[low];// <4> 低位不小于关键值的数赋予关键值的位置
}
data[low] = pivot; // 将key放在应排的位置
return low;
}
public static void main(String[] args) {
int[] arr = {6, 2, 1, 4, 8, 3, 0, 10, 69, 63, 316, 100, 7, 5, 103, 34};
// int[] arr = {21, 54, 2, 8, 90, 45, 27, 11, 88, 3, 64, 7, 22, 25, 99, 80};
// int[] arr = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16};
quickSort(arr, 0, arr.length - 1);
System.out.println(Arrays.toString(arr));
System.out.println(compareTimes);
}
}
堆排序
堆排序(heap sort),是指利用堆这种数据结构所设计的一种排序算法。
堆积是一个近似完全二叉树的结构,并同时满足堆积的性质,即子结点的键值或索引总是小于(或者大于)它的父节点。
堆排序是一种选择排序,它的最坏,最好,平均时间复杂度均为O(nlogn),它也是不稳定排序。
堆排序基本思想是将待排序序列构造成一个大顶堆,此时,整个序列的最大值就是堆顶的根节点。将其与末尾元素进行交换,此时末尾就为最大值。然后将剩余n-1个元素重新构造成一个堆,这样会得到n个元素的次小值。如此反复执行,便能得到一个有序序列了。
堆排序的步骤如下:
- 构造初始堆。将给定无序序列构造成一个大顶堆(一般升序采用大顶堆,降序采用小顶堆)。
- 将堆顶元素与末尾元素进行交换,使末尾元素最大。然后继续调整堆,再将堆顶元素与末尾元素交换,得到第二大元素。如此反复进行交换、重建、交换。
简单总结下堆排序的基本思路:
- 将无需序列构建成一个堆,根据升序降序需求选择大顶堆或小顶堆;
- 将堆顶元素与末尾元素交换,将最大元素“沉”到数组末端;
- 重新调整结构,使其满足堆定义,然后继续交换堆顶元素与当前末尾元素,反复执行调整+交换步骤,直到整个序列有序。